后缀数组

$sa[i]$：排名为$i$的后缀的位置

$rak[i]$：从第$i$个位置开始的后缀的排名，下文为了叙述方便，把从第$i$个位置开始的后缀简称为后缀$i$ $height[i]$:代表两个后缀的最长公共前缀的长度.

$s$：字符串,$s[i]$表示字符串中第$i$个字符串

以下模板可以求出:

1. 最长公共前缀，即height[]数组的值
2. 两个串的最长公共子串长度,复杂度$O(A+B)$
3. n个串的最长公共子串，具体的串
4. 一个串的不可重叠最长重复子串
5. 一个串的可重叠k次的最长重复子串
6. 求字符串不相同的子串个数

模板代码:复杂度$O(nlogn)$:

//调用需要注意.
//void da(原串，sa[],rak[],height[],原串长度,字符集大小)原串数组最后一位为0
int t1[N], t2[N], c[N], r[N], sa[N], rak[N], height[N];
bool cmp(int *r, int a, int b, int l)
{
    return r[a] == r[b] && r[a + l] == r[b + l];
}
void da(int str[], int sa[], int rak[], int height[], int n, int m)
{
    n++;
    int i, j, p, *x = t1, *y = t2;
    for (i = 0; i < m; i++)
        c[i] = 0;
    for (i = 0; i < n; i++)
        c[x[i] = str[i]]++;
    for (i = 1; i < m; i++)
        c[i] += c[i - 1];
    for (i = n - 1; i >= 0; i--)
        sa[--c[x[i]]] = i;
    for (j = 1; j <= n; j <<= 1)
    {
        p = 0;
        for (i = n - j; i < n; i++)
            y[p++] = i;
        for (i = 0; i < n; i++)
            if (sa[i] >= j)
                y[p++] = sa[i] - j;
        for (i = 0; i < m; i++)
            c[i] = 0;
        for (i = 0; i < n; i++)
            c[x[y[i]]]++;
        for (i = 1; i < m; i++)
            c[i] += c[i - 1];
        for (i = n - 1; i >= 0; i--)
            sa[--c[x[y[i]]]] = y[i];
        swap(x, y);
        p = 1;
        x[sa[0]] = 0;
        for (i = 1; i < n; i++)
            x[sa[i]] = cmp(y, sa[i - 1], sa[i], j) ? p - 1 : p++;
        if (p >= n)
            break;
        m = p;
    }
    int k = 0;
    n--;
    for (i = 0; i <= n; i++)
        rak[sa[i]] = i;
    for (i = 0; i < n; i++)
    {
        if (k)
            k--;
        j = sa[rak[i] - 1];
        while (str[i + k] == str[j + k])
            k++;
        height[rak[i]] = k;
    }
}

POJ2774 Long Long Message(后缀数组,最长公共子串)

两个串的最公共子串

因为height[]数组是由字典序相邻的后缀计算得到的，所以我们要从中剔除属于同一个串的。我们只需要判断(sa[i-1]>lena&&sa[i]<lena)||(sa[i-1]<lena&&sa[i]>lena)这样他们就属于两个串了，我们求出其中的height的最大值就是答案。

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 2e5 + 10;
-->模板代码
char s[N], a[N], b[N];
int main()
{
    //freopen("in.txt", "r", stdin);
    while (~scanf("%s%s", a, b))
    {
        int la = strlen(a), lb = strlen(b);
        for (int i = 0; i < la; i++)
            r[i] = a[i];
        r[la] = '#';
        for (int i = 0; i < lb; i++)
            r[i + la + 1] = b[i];
        r[la + lb + 1] = 0;
        int n = la + lb + 1;
        da(r, sa, rak, height, n, 128);
        int ans = 0;
        for (int i = 2; i <= n; i++)
            if (sa[i - 1] < la && sa[i] > la || sa[i - 1] > la && sa[i] < la)
                ans = max(ans, height[i]);
        printf("%d\n", ans);
    }

    return 0;
}

POJ3450 Corporate Identity(后缀数组,多个串的最长公共子串,二分)

给了n个字符串，求他们的最长公共子串。

1. 首先利用后缀数组计算出height[]数组。然后把所有的字符串连接起来，中间用#+i符号连接.
2. 用id[]数组记录每个字符所属的串的编号
3. 二分最长公共子串的长度，当相邻后缀的最长公共前缀连续大于二分的值k，且在所有串中都出现时，证明满足当前的条件.

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
#define mem(a, b) memset(a, b, sizeof(a))
const int N = 1e6 + 10;
模板代码
int n, res, a[N], id[N], vis[5000];
char s[N], ans[N];
bool check(int k)
{
    mem(vis, 0);
    int cnt = 0;
    for (int i = 2; i <= res; i++)
    {
        if (height[i] < k)
        {
            mem(vis, 0);
            cnt = 0;
            continue;
        }
        if (!vis[id[sa[i - 1]]])
        {
            vis[id[sa[i - 1]]] = 1;
            cnt++;
        }
        if (!vis[id[sa[i]]])
        {
            vis[id[sa[i]]] = 1;
            cnt++;
        }
        if (cnt == n)
        {
            for (int j = 0; j < k; j++)
            {
                ans[j] = a[sa[i] + j];
            }
            ans[k] = '\0';
            return true;
        }
    }
    return false;
}
int main()
{
    // freopen("in.txt", "r", stdin);
    while (scanf("%d", &n) && n)
    {
        res = 0;
        for (int i = 0; i < n; i++)
        {
            scanf("%s", s);
            int len = strlen(s);
            for (int j = 0; j < len; j++)
            {
                a[res] = s[j];
                id[res++] = i;
            }
            a[res] = '#' + i;
            id[res++] = '#' + i;
        }
        a[res] = 0;
        da(a, sa, rak, height, res, 5000);
        int l = 1, r = strlen(s), flag = 0;
        while (l <= r)
        {
            int mid = (l + r) >> 1;
            if (check(mid))
            {
                flag = 1;
                l = mid + 1;
            }
            else
                r = mid - 1;
        }
        if (flag)
            printf("%s\n", ans);
        else
            puts("IDENTITY LOST");
    }
    return 0;
}

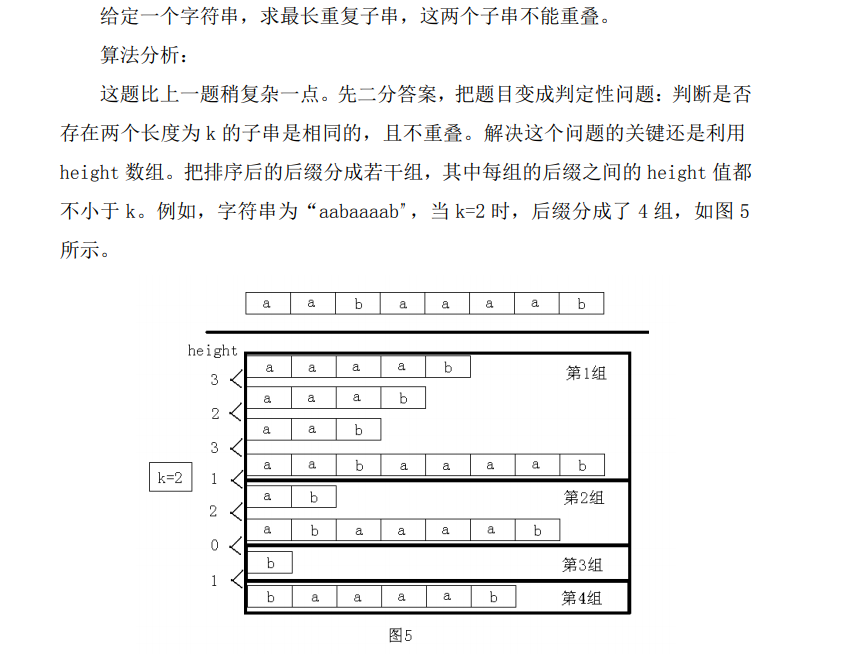
POJ1743 Musical Theme(后缀数组，不可重叠最长重复子串,二分)

给了一个长度为n的串,求这个数字串中长度最少为5的最长重复子串的长度（重复字串不需要完全相同但不能有重叠，只要某个字串同时加减一个相同的值后变为另一个字串即可） 输出该数字串中长度至少为5的最长重复子串的长度，如果不存在则输出0 。

1. 串不要求完全相同，可以通过字符的加减来进行，所以要进行预处理，计算出前缀差值，这样问题就变成了真正的重复子串问题
2. 二分最大长度k，然后按照k来分组
3. 找出每一组的sa的最大值和最小值，当MAX-MIN>=k的时候证明两个串不重叠，满足条件,如果所有组都不满足则不满足条件，注意这样算出的最长重复子串长度是差值串的，原串的最长重复字串长度还需要在这个基础上加一

附上论文题解:

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
#define mem(a, b) memset(a, b, sizeof(a))
const int N = 1e5 + 10;
模板代码
int n, res, a[N];
bool check(int k)
{
    int minn = sa[1], maxx = sa[1];
    for (int i = 2; i <= n; i++)
    {
        if (height[i] >= k && i < n)
        {
            minn = min(minn, sa[i]);
            maxx = max(maxx, sa[i]);
            continue;
        }
        if (maxx - minn >= k)
            return true;
        minn = maxx = sa[i]; //保证连续
    }
    return false;
}
int main()
{
    //freopen("in.txt", "r", stdin);
    while (scanf("%d", &n) && n)
    {
        for (int i = 0; i < n; i++)
            scanf("%d", &a[i]);
        for (int i = 0; i < n - 1; i++)
            a[i] = a[i + 1] - a[i] + 100;
        a[--n] = 0;
        da(a, sa, rak, height, n, 200);
        int l = 4, r = n, ans = 0;
        while (l <= r)
        {
            int mid = (l + r) >> 1;
            if (check(mid))
            {
                ans = mid;
                l = mid + 1;
            }
            else
                r = mid - 1;
        }
        ans++;
        printf("%d\n", ans >= 5 ? ans : 0);
    }

    return 0;
}

POJ3261 Milk Patterns(后缀数组,可重叠k次最长重复子串,二分)

给定一个字符串，求至少出现 k 次的最长重复子串，这 k 个子串可以重叠。

和POJ1743思路基本一样，都是求最长重复子串，不同的是这个题加了条件，要求：

1. 字符串可以重叠
2. 出现次数>=k

我们同样采取二分的方法，首先按照二分的长度mid进行分组，使得每一个组中相邻后缀的最长公共前缀的值都>=mid(就是height[i]>=mid),那么只要有一个组中元素的数量>=k时就满足情况

论文题解:

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
#define mem(a, b) memset(a, b, sizeof(a))
const int N = 1e5 + 10;
模板代码
int n, a[N], k;
bool check(int mid)
{
    int cnt = 1;
    for (int i = 2; i <= n; i++)
    {
        if (height[i] >= mid)
        {
            cnt++;
            continue;
        }
        if (cnt >= k)
            return true;
        cnt = 1;
    }
    if (cnt >= k)
        return true;
    return false;
}
int main()
{
    // freopen("in.txt", "r", stdin);
    while (~scanf("%d%d", &n, &k))
    {
        int temp = 0;
        for (int i = 0; i < n; i++)
        {
            scanf("%d", &a[i]);
            temp = max(temp, a[i]);
        }
        a[n] = 0;
        da(a, sa, rak, height, n, temp + 1);
        int l = 0, r = n, ans = 0;
        while (l <= r)
        {
            int mid = (l + r) >> 1;
            if (check(mid))
            {
                ans = mid;
                l = mid + 1;
            }
            else
                r = mid - 1;
        }
        printf("%d\n", ans);
    }
    return 0;
}
/*
8 2
2 6 8 3 9 1 7 5 
8 2
2 7 3 3 8 8 8 8 
*/

SPOJ Distinct Substrings (后缀数组，不相同的子串个数)

给出一个字符串，求其中不同的子串个数.

一个串的子串个数为n*(n+1)/2，减去后缀的相同前缀所作的贡献每一个height[i]即为答案.

引用论文:

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
#define mem(a, b) memset(a, b, sizeof(a))
const int N = 1e5 + 10;
模板代码
char s[N];
int a[N];
int main()
{
    //freopen("in.txt", "r", stdin);
    int t;
    scanf("%d", &t);
    while (t--)
    {
        scanf("%s", s);
        int n = strlen(s);
        for (int i = 0; i < n; i++)
            a[i] = s[i];
        a[n] = 0;
        da(a, sa, rak, height, n, 128);
        int ans = n * (n + 1) / 2;
        for (int i = 2; i <= n; i++)
            ans -= height[i];
        printf("%d\n", ans);
    }
    return 0;
}