容斥原理总结
概述:
先引入百度百科的定义:
在计数时,必须注意没有重复,没有遗漏。为了使重叠部分不被重复计算,人们研究出一种新的计数方法,这种方法的基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。
一般可以描述如下:
要计算几个集合并集的大小,我们要先将所有单个集合的大小计算出来,然后减去所有两个集合相交的部分,再加回所有三个集合相交的部分,再减去所有四个集合相交的部分,依此类推,一直计算到所有集合相交的部分。
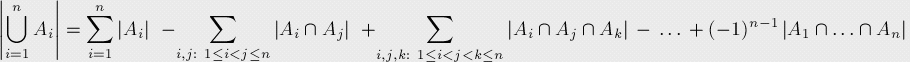
用韦恩图来表示:
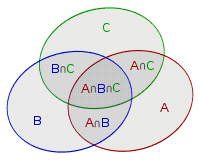
上图就可以表示为:|A∪B∪C| = |A|+|B|+|C| - |A∩B| - |B∩C| - |C∩A| + |A∩B∩C|
例如:
给你一个数,问从1~n中与互质的数有多少个。
假设,我们可以先求出30的质因数,30的质因数为:2,3,5
那么我们就可以看成是3个集合,集合中的元素分别为2,3,5,全集就为从1~30中的所有数
所以我们就从中减去2的倍数,3的倍数,5的倍数,但是6既是2的倍数也是3的倍数,被多算了一次,所以要减去6的倍数,同理减去的倍数,的倍数,最后加上的倍数,用数学公式表达为:
所以在1~30中与30互质的数有8个.
这个问题实际上也正是欧拉函数解决的问题,请看欧拉函数
模板
int a[50],b[1010];//a保存n的质因子,a[0]表示质因子个数
void div(int n)//分解质因数
{
int j=0;
for(int i=2; i*i<=n; i++)
if(n%i==0)
{
while(n%i==0)
n/=i;
a[++j]=i;
}
if(n>1) a[++j]=n;
a[0]=j;
}
int get_cnt(int mid)//1--mid之间与n互质的数有多少个
{
int g=0,sum=mid,t;
b[++g]=1;
for(int i=1; i<=a[0]; i++)
{
t=g;
for(int j=1; j<=g; j++)
{
b[++t]=b[j]*a[i]*-1;
sum+=mid/b[t];
}
g=t;
}
return sum;
}
例题
-
这就是上面讲的那个题意了,给你一个数,问从
1~n中与互质的数有多少个。typedef long long ll; #define inf 1000000 #define mem(a,b) memset(a,b,sizeof(a)) int a[50],b[1010];//a保存n的质因子,a[0]表示质因子个数 void div(int n)//分解质因数 { int j=0; for(int i=2; i*i<=n; i++) if(n%i==0) { while(n%i==0) n/=i; a[++j]=i; } if(n>1) a[++j]=n; a[0]=j; } int get_cnt(int mid)//1--mid之间与n互质的数有多少个 { int g=0,sum=mid,t; b[++g]=1; for(int i=1; i<=a[0]; i++) { t=g; for(int j=1; j<=g; j++) { b[++t]=b[j]*a[i]*-1; sum+=mid/b[t]; } g=t; } return sum; } int main() { int t,n; scanf("%d",&t); while(t--) { mem(a,0);mem(b,0); scanf("%d",&n); div(n); printf("%d\n",get_cnt(n)); } return 0; } -
题目给出了,求有多少对(),满足,后台数据保证了和的值都为1,所以题目转化成求:从中和中满足的的对数。
那么题目就可进一步转化为求从和中有多少对满足(互质)的对数。
为了方便计算,我们在输入的时候进行处理,使得
b<=d,那么,我们只需要从中枚举,找到在中与互质的数的个数:- 当时枚举的数会重复,所以要去重
- 当时直接利用容斥原理枚举,最后两次枚举的和就是答案
ll a[50],b[1010];//a保存n的质因子,a[0]表示质因子个数 void div(ll n)//分解质因数 { ll j=0; for(ll i=2; i*i<=n; i++) if(n%i==0) { while(n%i==0) n/=i; a[++j]=i; } if(n>1) a[++j]=n; a[0]=j; } ll get_cnt(ll mid)//1--mid之间与n互质的数有多少个 { ll g=0,sum=mid,t; b[++g]=1; for(ll i=1; i<=a[0]; i++) { t=g; for(ll j=1; j<=g; j++) { b[++t]=b[j]*a[i]*-1; sum+=mid/b[t]; } g=t; } return sum; } int main() { ll a,b,c,d,t,q=1,k; scanf("%lld",&t); while(t--) { scanf("%lld%lld%lld%lld%lld",&a,&b,&c,&d,&k); printf("Case %lld: ",q++); if(k==0) { puts("0"); continue; } ll sum=b+d; b=min(b,d); d=sum-b; a=b/k,c=d/k; ll ans=0; for(ll i=1; i<=a; i++) { div(i); ans+=get_cnt(a);//从1~a中与i互质的数的个数 } ans=(ans+1)/2; for(ll i=a+1; i<=c; i++) { div(i); ans+=get_cnt(a); } printf("%lld\n",ans); } return 0; }
题目转化一下就可以变成:已知x∈[1,n],y∈[1,m]求x和y这两个集合中互质的数的个数。利用容斥,枚举x集合,然后暴力加起来
ll a[50],b[1010];//a保存n的质因子,a[0]表示质因子个数
void div(ll n)//分解质因数
{
ll j=0;
for(ll i=2; i*i<=n; i++)
if(n%i==0)
{
while(n%i==0)
n/=i;
a[++j]=i;
}
if(n>1) a[++j]=n;
a[0]=j;
}
ll get_cnt(ll mid)//1--mid之间与n互质的数有多少个
{
ll g=0,sum=mid,t;
b[++g]=1;
for(ll i=1; i<=a[0]; i++)
{
t=g;
for(ll j=1; j<=g; j++)
{
b[++t]=b[j]*a[i]*-1;
sum+=mid/b[t];
}
g=t;
}
return sum;
}
int main()
{
ll t,n,m;
scanf("%lld",&t);
while(t--)
{
mem(a,0);
mem(b,0);
ll ans=0;
scanf("%lld%lld",&n,&m);
for(ll i=1; i<=n; i++)
{
div(i);
ans+=get_cnt(m);
}
printf("%lld\n",ans);
}
return 0;
}
题目给出了一个区间[a,b]和一个数n,让你求出a~b中与n互质的数的个数,我们只需要求出从1~b与n互质的数的个数减去从1~a中与n互质的数的个数
ll a[50],b[1010];//a保存n的质因子,a[0]表示质因子个数
void div(ll n)//分解质因数
{
ll j=0;
for(ll i=2; i*i<=n; i++)
if(n%i==0)
{
while(n%i==0)
n/=i;
a[++j]=i;
}
if(n>1) a[++j]=n;
a[0]=j;
}
ll get_cnt(ll mid)//1--mid之间与n互质的数有多少个
{
ll g=0,sum=mid,t;
b[++g]=1;
for(ll i=1; i<=a[0]; i++)
{
t=g;
for(ll j=1; j<=g; j++)
{
b[++t]=b[j]*a[i]*-1;
sum+=mid/b[t];
}
g=t;
}
return sum;
}
int main()
{
ll t,q=1,a,b,n;
scanf("%lld",&t);
while(t--)
{
scanf("%lld%lld%lld",&a,&b,&n);
div(n);
printf("Case #%lld: %lld\n",q++,get_cnt(b)-get_cnt(a-1));
}
return 0;
}
首先我们可以利用容斥原理知道:1~m(m为任意值)中与n互质的数的个数
然后考虑利用二分查找数字,然后判断这个数字和n有多少个互质数
int a[50],b[1010];//a保存n的质因子,a[0]表示质因子个数
void div(int n)//分解质因数
{
int j=0;
for(int i=2; i*i<=n; i++)
if(n%i==0)
{
while(n%i==0)
n/=i;
a[++j]=i;
}
if(n>1) a[++j]=n;
a[0]=j;
}
int get_cnt(int n)//容斥原理来判断二分的mid有多少个与n互质的数
{
int g=0,sum=n,t;
b[++g]=1;
for(int i=1; i<=a[0]; i++)
{
t=g;
for(int j=1; j<=g; j++)
{
b[++t]=b[j]*a[i]*-1;
sum+=n/b[t];
}
g=t;
}
return sum;
}
int erfen(int n,int k)
{
int mid,l=1,r=(int)2e9;
while(l<=r)
{
mid=(l+r)>>1;
if(get_cnt(mid)<k)
l=mid+1;
else
r=mid-1;
}
return l;
}
int main()
{
int n,k;
while(~scanf("%d%d",&n,&k))
{
div(n);
printf("%d\n",erfen(n,k));
}
return 0;
}