网络流
给定指定的一个有向图,其中有两个特殊的点源S(Sources)和汇T(Sinks),每条边有指定的容量(Capacity),求满足条件的从S到T的最大流(MaxFlow).
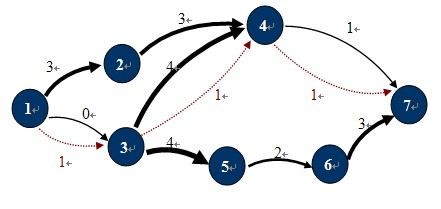
网络流相关定义
- 网络是一个有向带权图,包含一个源点和一个汇点,没反平行边
- 网络流:即网络上的流,是定义在边集E上的一个非负函数$flow={flow(u,v)}$,$flow(u,v)$是边上的流量
- 可行流:满足容量约束和流量守恒的网络流
- 网络最大流:满足容量约束和流量守恒的条件下,在流网络中找到一个净输出最大的网络流
最大流
求解最大流的整体思路是福特福克森算法。该算法的思想是: 在残余网络中找可增广路,然后在实流网络中沿着可增广路增流,在残余网络中沿着可增广路减流,;继续在残余网络中找可增广路。直到不存在可增广路位置。此时,实流网络中的可行流就是所求的最大流.
增广路定理:设$flow$是网络$G$的一个可行流,如果不存在从源点$S$到汇点$t$关于$flow$的可增广路$p$,则$flow$是$G$的一个最大流
福特福克森也是能算是一种求解最大流的思想,并不是具体的算法。下面说一下具体实现的算法。 实现的算法有三种:EK算法,Dinic算法,SAP算法+gap优化
最大流最小割定理
主要是理解一些概念
- 割:设Ci为网络N中一些弧的集合,若从N中删去Ci中的所有弧能使得从源点Vs到汇点Vt的路集为空集时,称Ci为Vs和Vt间的一个割。就是用一条线可以把一张有向图分割成两个不想交的集合,割的容量就是这一条线割到的边上的容量之和
- 最小割:图中所有的割中,边权值和最小的割为最小割。就是用一条线把一个图分成两个部分,使得边上所有容量的和最小,如下图最小割的容量为:5+4+2=11
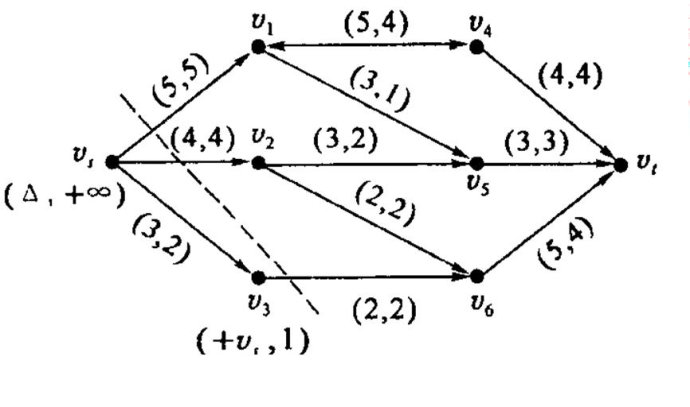
- 最大流最小割定理:在任何的网络中,最大流的值等于最小割的容量。否则还可以增广。那么有一个特征:最小割个到的边的容量和流量相等。