图的连通-tarjan算法
绪论
学习了一周图的连通性问题,现在总结一下关于图的连通性问题。图的连通性问题一般分为以下几种:
- 无向图求关节点(割点)
- 无向图求桥(割边)
- 无向图的点双连通分量
- 无向图的边双联通分量
- 有向图求强连通分量
还需要注意一些v==fa的问题:
- 强连通分量(不用判断)
- 割点(不用判断)
- 求割边或者边双连通分量的时候,用
flag或者i==fa^1来去重边,在用i==fa^1的时候,需要注意在传参的时候要tarjan(v,i)而不是tarjan(v,u) - 强连通分量(不用判,只有无向图有这个问题,有向图不存在)
在求的这些问题中,有一些技巧来应对不同的情况:
low数组的问题:
关于tarjan算法,一直有一个很大的争议,就是low[u]=min(low[u],dfn[v]); 这句话,如果改成low[u]=min(low[u],low[v])就会wa掉,但是在求强连通分量时却没有问题 ①根据许多大佬的观点,我想提出自己的一点看法,在求强连通分量时,如果v已经在栈中,那么说明u,v一定在同一个强连通分量中,所以到最后low[u]=low[v]是必然的,提前更新也不会有问题,但是在求割点时,low的定义有了小小的变化,不再是最早能追溯到的祖先,(因为是个无向图)没有意义,应该是最早能绕到的割点,为什么用绕到,是因为是无向边,所以有另一条路可以走,如果把dfn[v]改掉就会上翻过头,可能翻进另一个环中,所以wa掉(转自洛谷) ②low[u]=min(low[u],dfn[v])中的dfn[v]可不可以改成low[v]呢,答案是不可以,当你从u访问v到,发现v被访问过的时候,v的low值不一定确定了,说不定只有一个暂时的值而已,也就是:tmpdfn=lastdfn tmplow!=lastlow,所以不能代替。(转自Acfun栗主席)
结论:
- 所以在在求强连通分量的时候,可以用
low[v]代替,dfn[v ],但是一般情况下还是不要改
缩点的问题
- 在缩点的时候通常会借用一个
color数组,在满足low[u]==dfn[u]的时候,证明有了一个连通分量,这个时候用color来标记一下当前这个点所在的连通分量的集合 - 在无向连通图中,可以用
low数组来代替染色,因为在无向图中同一个连通分量里的low值相等,最好染色,不会出错
无向图判重边的方法
采用kuangbin的判重边方法,还不错
void tarjan(int u,int fa)
{
int flag=0;
vis[u]=1;
s.push(u);
dfn[u]=low[u]=++times;
for(int i=first[u]; ~i; i=e[i].next)
{
int v=e[i].v;
if(v==fa&&!flag)
{
flag=1;
continue;
}
if(!dfn[v])
{
tarjan(v,u);
low[u]=min(low[u],low[v]);
if(low[v]>dfn[u])
{
minn=min(minn,e[i].w);
}
}
else if(vis[v])
low[u]=min(low[u],dfn[v]);
}
if(low[u]==dfn[u])
{
cnt++;
while(1)
{
int now=s.top();
s.pop();
color[now]=cnt;//染色
num[cnt]++;//记录同一个分量中顶点的个数
vis[now]=0;
if(now==u) break;
}
}
}
用了一个flag数组来标记
无向图求割点
在Tarjan的算法的过程中,只要满足low[v]>=dfn[u]就可有判断有割点,不过需要注意的是,判断根节点是不是割点的时候需要判断它的儿子数>=2,因为儿子大于等于2时,才是割点,所以要对于根节点进行特判。
以洛谷P3388(求割点模板题)为例:
const int N=100000+7;
const int M=2*100000+20;
int dfn[N],low[N],times;
int root,son;
int n,m;
int first[N],tot,subnets[N];
struct edge
{
int v;
int next;
} e[M];
void add_edge(int u,int v)
{
e[tot].v=v;
e[tot].next=first[u];
first[u]=tot++;
}
void init()
{
mem(dfn,0);
mem(low,0);
mem(first,-1);
mem(subnets,0);
tot=0;
times=0;
}
void tarjan(int u)
{
low[u]=dfn[u]=++times;
for(int i=first[u]; ~i; i=e[i].next)
{
int v=e[i].v;
if(!dfn[v])
{
tarjan(v);
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u])
{
if(u==root)
son++;
else
subnets[u]++;
}
}
else
low[u]=min(low[u],dfn[v]);
}
}
int main()
{
int u,v;
init();
scanf("%d%d",&n,&m);
for(int i=1; i<=m; i++)
{
scanf("%d%d",&u,&v);
add_edge(u,v);
add_edge(v,u);
}
for(int i=1; i<=n; i++)
if(!dfn[i])
{
root=i;
son=0;
tarjan(i);
if(son>1)
subnets[i]=1;
}
int sum=0;
for(int i=1; i<=n; i++)
if(subnets[i])
sum++;
printf("%d\n",sum);
for(int i=1; i<=n; i++)
if(subnets[i])
printf("%d ",i);
return 0;
}
无向图求割边
求割边和求割点基本一样,不用做什么改变,只需要把low[v]>=dfn[u]改成low[v]>dfn[u]就行了,代码和上面的求割边基本一样,就不写了
点双连通图
一个无向图如果没有关节点(割点),或者或是连通度大于1(),则称为点双连通图 概念可以看这里: 图的割点、桥与双连通分支
边双连通图
一个无向图如果没有桥(割边),则称为边双连通图
强连通分量
关于求解强连通分量的Tarjan算法,可以看一下这个博客:有向图强连通分量的Tarjan算法
求强连通分量的关键在于判断:low[u]==dfn[u],当出现这个条件的时候,就证明他找到了一个环,这个时候栈中的元素就是当前点所在的强连通分量
以UOJ146为例,这是一个强连通分量的模板题
#include <bits/stdc++.h>
using namespace std;
#define inf 0x3f3f3f3f
#define mem(a,b) memset(a,b,sizeof(a))
const int N=2e5+7;
vector<int>e[N];
int dfn[N],low[N],tot,n,ans,vis[N];
stack<int>s;
void tarjan(int u)
{
low[u]=dfn[u]=tot++;
s.push(u);
vis[u]=1;
for(int i=0; i<e[u].size(); i++)
{
int v=e[u][i];
if(!dfn[v])
{
tarjan(v);
low[u]=min(low[u],low[v]);
}
else if(vis[v])
low[u]=min(low[u],dfn[v]);
}
if(low[u]==dfn[u])
{
int cnt=0;
while(1)
{
int now=s.top();
s.pop();
vis[now]=0;
cnt++;
if(now==u) break;
}
if(cnt>1) ans=min(ans,cnt);
}
}
void init()
{
tot=0;
ans=inf;
mem(vis,0);
mem(dfn,0);
mem(low,0);
for(int i=1; i<=n; i++)e[i].clear();
while(!s.empty())s.pop();
}
int main()
{
int x;
scanf("%d",&n);
init();
for(int i=1; i<=n; i++)
{
scanf("%d",&x);
e[i].push_back(x);
}
for(int i=1; i<=n; i++)
if(!dfn[i])
tarjan(i);
printf("%d\n",ans);
return 0;
}
这道题是强连通分量模板题,只需要判断强连通分量的个数是否为1,就可以。需要用到Tarjan算法
//这道题只需要记录强连通分量的个数,所以可以不需要栈以及vis数组
#define mem(a,b) memset(a,b,sizeof(a))
typedef long long ll;
const int N=10000+2;
const int M=100000+2;
int dfn[N],low[N],vis[N],times,cnt;
stack<int>s;//标记一个强连通分量中的点
int first[N],tot;
struct edge
{
int v,next;
} e[M];
void add_edge(int u,int v)
{
e[tot].v=v;
e[tot].next=first[u];
first[u]=tot++;
}
void init()
{
mem(dfn,0);
mem(low,0);
mem(vis,0);
mem(first,-1);
times=0;
tot=0;
cnt=0;
while(!s.empty())s.pop();
}
void tarjan(int u)
{
vis[u]=1;
s.push(u);
dfn[u]=low[u]=++times;
for(int i=first[u]; ~i; i=e[i].next)
{
int v=e[i].v;
if(!dfn[v])
{
tarjan(v);
low[u]=min(low[u],low[v]);
}
else if(vis[v])
low[u]=min(low[u],dfn[v]);
}
if(low[u]==dfn[u])
{
cnt++;
while(1)
{
int now=s.top();
s.pop();
vis[now]=0;
if(now==u) break;
}
}
}
int main()
{
int n,m,a,b;
while(scanf("%d%d",&n,&m)&&(n||m))
{
init();
for(int i=1; i<=m; i++)
{
scanf("%d%d",&a,&b);
add_edge(a,b);
}
for(int i=1; i<=n; i++)
if(!dfn[i])
tarjan(i);
puts(cnt==1?"Yes":"No");
}
return 0;
}
POJ1236 Network of Schools(图的强连通分量,Tarjan算法)
首先说明题意,有n个学校,现在有一款软件,需要分发给一些学校,这些学校分别和其他学校连接着一些网络,可以通过网络可以直接把软件传输给另一个学校(A连接B学校但是B不一定连接A学校),现在有两个问题:
- 需要至少准备多少个软件的备份,可以是使所有的学校都能接受的备份。
- 至少需要连多少条边,只需要给网络中的任意一个学校发放软件,其他所有的学校都可以接收到。
那么我们先考虑,在图中找到一个强连通分量,因为强连通分量中的点,每两点之间任意都可达,所以只要其他点连接到强连通分量中的点,就可以满足题目所需的条件。那么我们现在考虑缩点,把强连通分量中的点缩成同一个点,以样例来说明,如图:
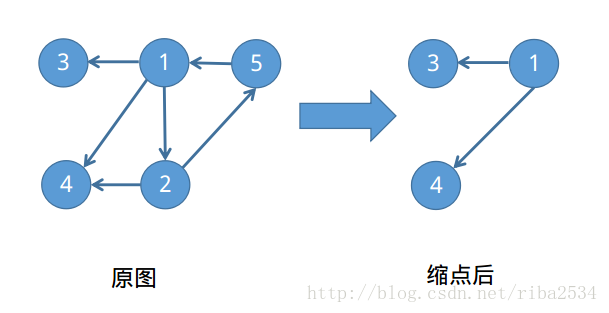
从图上可以看出我们只需要准备两份软件的拷贝,就可以满足条件1,也就是说统计一下入度为0的点的个数
条件2问的是最少加几条边可以使整个图变成任意两点可达,那么我们考虑一下强连通图的性质:
- 每个顶点的出度和入度都不等于0
根据这个性质,我们算出来出度为0的点有多少条,入度为0的点有多少条,从里面找出最大值即可。
#define mem(a,b) memset(a,b,sizeof(a))
typedef long long ll;
const int N=100+2;
const int M=N*N;
int dfn[N],low[N],vis[N],times,cnt;
int color[N];//缩点用
int in[N],out[N];//入度和出度点的个数
stack<int>s;//标记一个强连通分量中的点
int first[N],tot;
struct edge
{
int v,next;
} e[M];
void add_edge(int u,int v)
{
e[tot].v=v;
e[tot].next=first[u];
first[u]=tot++;
}
void init()
{
mem(dfn,0);
mem(low,0);
mem(vis,0);
mem(first,-1);
mem(color,0);
mem(in,0);
mem(out,0);
times=0;
tot=0;
cnt=0;
while(!s.empty())s.pop();
}
void tarjan(int u)
{
vis[u]=1;
s.push(u);
dfn[u]=low[u]=++times;
for(int i=first[u]; ~i; i=e[i].next)
{
int v=e[i].v;
if(!dfn[v])
{
tarjan(v);
low[u]=min(low[u],low[v]);
}
else if(vis[v])
low[u]=min(low[u],dfn[v]);
}
if(low[u]==dfn[u])
{
cnt++;
while(1)
{
int now=s.top();
s.pop();
color[now]=cnt;
vis[now]=0;
if(now==u) break;
}
}
}
int main()
{
int v,n;
while(~scanf("%d",&n))
{
init();
for(int u=1; u<=n; u++)
while(scanf("%d",&v)&&v)
add_edge(u,v);
for(int i=1; i<=n; i++)
if(!dfn[i])
tarjan(i);
if(cnt==1)
{
printf("1\n0\n");
continue;
}
for(int u=1; u<=n; u++)
{
for(int j=first[u]; ~j; j=e[j].next)
{
v=e[j].v;
if(color[u]!=color[v])
{
in[color[v]]++;//v的入度
out[color[u]]++;//u的出度
}
}
}
int a=0,b=0;
for(int i=1; i<=cnt; i++)
{
if(!in[i])a++;
else if(!out[i])b++;
}
printf("%d\n%d\n",a,max(a,b));
}
return 0;
}